モンテカルロ・シミュレーション

シミュレーションには、不規則性を導入したい場合が少なくありません。たとえば、荷電粒子の運動は規則性なくランダムが動くため、これを完全にモデル化することは困難です。また、渋滞のシミュレーションなどは、計算過程で不規則性を導入して実際の運転者の動きを模擬します。

モンテカルロ・シミュレーション (Monte Carlo Simulation) は、シミュレーションに不規則性を導入する際に用いられる代表的な方法です。モンテカルロ・シミュレーションは、モンテカルロ法 (Monte Carlo method) をもとに現象の統計的特性を得るためサンプリングを繰り返し行います。モンテカルロ法は、ある不確実な事象について起こりうる結果を確率分布を用いて推定するための数学的技法です。確率分布は不確実性を持つ変数をモデル化するために利用され、シミュレーションの仕組みとしては乱数を用います。

　　　　　図：モンテカルロ・シミュレーションを用いたランダム・ウォークの模擬

モンテカルロ・シミュレーションは、不確実な状況下でより良い意思決定を行うために、第二次世界大戦中にStanislaw Ulamによって考案されました。 John von Neumannによって、カジノで有名な国家モナコ公国のモンテカルロから名付けられました。 1948年には、当時のスーパーコンピュータであるENIACで核分裂に関する数値解析に、モンテカルロ・シミュレーションが利用されたそうです¹。現在も、人工知能、株価、販売予測、プロジェクト管理、価格設定など、多くの現実的なシナリオにおけるリスクの影響の評価に用いられています。

モンテカルロ法とモンテカルロ・シミュレーションは、あまり区別しないで使われることも多いですが、傾向は以下のようになっています。

モンテカルロ法：数学的・統計的な問題を解決するために使われる数学的な手法自体を指す
モンテカルロ・シミュレーション：ある現象の統計的特性を得るためサンプリングを多数回行うシミュレーション手法を指す

モンテカルロ法

モンテカルロ法の基本的な考え方は、ある入力の集団からサンプルをランダムに抽出して決定論的に出力を求め、その試行を大量に行った結果を統計分析するものです。一般的なシミュレーション・モデルとは異なり、固定入力値のセットの代わりに一連の推定値を使用して、一連の結果を予測します。言い換えると、モンテカルロ法は固有の不確実性を持つ任意の変数を確率分布で代用して、発生可能な結果のモデルを構築します。

モンテカルロ法に厳密な定義はありませんが、多くの場合は以下の様な手順から成っています。

乱数を利用してランダムサンプリングを行い、入力とする
1で生成された値と作成したモデルを用いて、決定論的に問題を解いたり値を計算する
1,2を多数回行う
計算結果を統計的に処理して、求めたい量を推定する

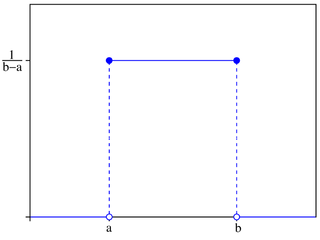
モンテカル法は、必ずしも純粋な乱数を必要としません。多くの場合、良いシミュレーションを行うために必要な乱数は、シミュレーション対象から見て十分にランダムな乱数です。例えば、「ランダムサンプリングで得られた一連の入力値が、一様分布や正規分布などの形を取っているかどうか？」などが基準として用いられます。つまり、乱数の分布が一様分布や正規分布などの形を取っていれば大丈夫と言えます。典型的な例では、真の乱数ではなく疑似乱数が用いられ、数千個の乱数を発生させて計算を行うため、計算に非常に時間がかかります。

![](figures/05_monte_carlo_method_2023-05-13-14-32-20.png){:style="height:200px"}

図：連続一様分布² 図：正規分布³

代表例

サイコロ

モンテカルロ法の単純な例として、サイコロを振って出る目の確率と分布を見てみましょう。サイコロは1～6の目がありますので、1～6をJuliaのrand関数⁵で発生させ、ヒストグラムにしてみます。

サイコロの出目の分布を見るjuliaコード

number_of_throw = parse(Int64, Base.prompt("Please set the number of throws"))
throw_dice = rand(1:6, number_of_throw)
histogram(throw_dice, title="Throwing dice $(number_of_throw) time", bins=6, normalize=:pdf)
savefig("histogram_throw_dice.png")

実行例

上記のJuliaコードを"throw_dice.jl"というファイルとして保存し、includeするとhistogram_throw_dice.pngという画像ファイルが生成される。

julia> include("throw_dice.jl")
Please set the number of throws: 1000
"/root/histogram_throw_dice.png"

サイコロを振る回数、つまり乱数を使って試行する回数、を増やすと分布が一様なものになっていくのがわかります。

　　　　
　　　　図：10回　　　　　　　　　　図：100回　　　　　　　　図：1000回

ビュフォンの針

ビュフォンの針 (Buffon's needle problem) は、18世紀の博物学者 Georges-Louis Leclerc, Comte de Buffon によって提起された以下の様な数学上の問題です。

多数の平行線が引かれた床に針を落したとき、どれかの線と針が交差する確率は何%か？

より数学的にこの問題を設定すると、答えは以下のようになります。

平行線の間隔： $d$
針の長さ： $l ~(<= d)$
針が線と交わる確率： $\displaystyle \frac{2l}{\pi d}$

　　　　　　　　　　　　　　　　　　　図：ビュフォンの針

針は平行線に無作為に落とすので、その位置と角度はそれぞれ一様分布に従っていると考えられます。この問題を用いて、円周率を近似することができます。詳しくは、参考文献⁶⁷を見てください。

疑似乱数

モンテカルロ法は、入力値に用いられる乱数が結果を大きく左右します。計算機を用いて乱数を発生やその性質は広く研究されてきました。

疑似乱数 (Pseudo-Random Number) は、決定論的アルゴリズムによって生成され、ある区間上で独立かつ一様に分布する数列のことです。また、これを計算機などを用いて生成するアルゴリズムを疑似乱数生成器 (Pseudo-Random Number Generator, PRNG) と呼びます。代表的な疑似乱数生成器に、線形合同法やメルセンヌ・ツイスター、Xorshiftがあります。

　　
　　　　図：線形合同法　　　　　　　　　図：メルセンヌ・ツイスタ

疑似乱数は真の乱数ではありませんが、だからと言って真の乱数より劣っているということはありません。なお、真の乱数とは以下の3つの性質を満たしたものを言います。真の乱数は規則性も再現性もないため、シミュレーションには利用しにくいです。

無作為性：統計的な偏りがなく、規則性もない性質
予測不可能性：過去に生成された値から次に生成される値が予測できない性質
再現不可能性：特定の数列を出力できないという性質

疑似乱数はこの条件を満たしません。とくに予測不可能性と再現不可能性は満たしませんが、シミュレーションではそれをうまく利用します。例えば、擬似乱数は確定的な計算によって生成するため、生成法と内部状態が既知であれば、生成される値が予測可能です。予想可能であれば、生成器を調整することにより、全体として一様分布や正規分布になるような数列を作ることができます。

疑似乱数を生成する際の評価基準には、以下の様なものがあります。

周期：過去に生成した値と同じ値が再び生成される長さのこと。長いと良い
分布：生成される値が一様で偏りが無いこと
生成速度：乱数を生成するのにかかるコストのこと。小さいと良い

疑似乱数をモンテカルロ・シミュレーションなどに利用する場合は、ある範囲で生成された数列がランダムに見えれば問題ありません。しかし、ある擬似乱数がある範囲で真の乱数とみなして良いかを決定する確実な方法はありません。そのため、利用する乱数の統計的な性質を、目的に合致しているかどうかを判断する検定と呼ばれる作業が必要になります。

線形合同法

線形合同法 (Linear Congruential Generator) は、最も有名な疑似乱数発生法の1つです⁸⁹。乱数の発生方法は以下の手順をとり、古代のC言語などの擬似乱数関数 rand()はこの方法をもとに作られています。

ある整数 $R_{1}$ を初期値（シード）として選ぶ
以下のような漸化式を用いて乱数を順に生成。 $a, C, m$ は正の整数。

$R_{i+1} = (a \times R_{i} + C) \mod m$

線形合同法が生成する乱数は、現代では使うべきではありません¹⁰¹²¹³。これは、初期シードの選び方によらず周期が最大で $2^{32}$ と非常に短かいことや、生成された数字を $\mod 偶数$ した場合は偶数と奇数が必ず交互に現れるなど分布に問題があるためです。

以下の例では、 $a = 1664525, C = 1013904223, m = 2^{32}$ として、1～7の数字を作るコードと実行例を示しています。 7, 2, 1, 4, 3, 6, 5, 0を繰り返してしまっており、ひとめで乱数としては不適切なことがわかります。

線形合同法のjuliaコード

const LIMIT = 100 #2^(32)
r = parse(Int32, Base.prompt("Please set the initial value."))
for i in 1:LIMIT
        global r = mod(1664525 * r + 1013904223, 2^32)
        print(r%7, ", ")
end

実行例

julia> Please set the initial value.: 0
7, 2, 1, 4, 3, 6, 5, 0, 7, 2, 1, 4, 3, 6, 5, 0, 7, 2, 1, 4, 3, 6, 5, 0, 7, 2, 1, 4, 3, 6, 5, 0, 7, 2, 1, 4, 3, 6, 5, 0, 7, 2, 1, 4, 3, 6, 5, 0, 7, 2, 1, 4, 3, 6, 5, 0, 7, 2, 1, 4, 3, 6, 5, 0, 7, 2, 1, 4, 3, 6, 5, 0, 7, 2, 1, 4, 3, 6, 5, 0, 7, 2, 1, 4, 3, 6, 5, 0, 7, 2, 1, 4, 3, 6, 5, 0, 7, 2, 1, 4,

メルセンヌ・ツイスター

メルセンヌ・ツイスター (Mersenne twister) は、現在でも使われている最も有名な擬似乱数列生成器の1つで、1996年に松本眞と西村拓士によって提案されました⁸。メルセンヌ・ツイスターはいくつかの実装がありますが、最もよく使われるアルゴリズムは32bitの $2^{19937} - 1$ というメルセンヌ素数にもとづいており、"MT19937"などと表記されます。この他、64bit版のMT19937-64という実装も存在します。

メルセンヌ・ツイスターの特徴は以下のようなもので、他の乱数生成手法に存在する欠点を克服し、高品質かつ高速に乱数を生成できることです。また、ソースコードがホームページで公開されています。⁹

利点

周期：非常に長い。 $2^{19937} - 1 \simeq 4.3 \times 106001$
分布：非常に広い。32bit精度で1周期で623次元空間に均等分布。
生成速度：大きいサイズの線形合同法（ $2^48$ ）よりも高速

欠点

2.5KiBという比較的大きな状態バッファを持つ
現代の基準では中途半端なスループットである
変種を使用しない限り、暗号への適用には安全ではない

メルセンヌ・ツイスタ(Mersenne Twister)法まとめ - あつまれ統計の森に掲載されている、メルセンヌ・ツイスタのPythonプログラムをJuliaに移植したものを以下に示します。

メルセンヌツイスタと生成した乱数の分布を見るjuliaコード

using Random
using Plots

const N = 624
const M = 397
# constant vector a
const a = 0x9908b0df

numbers = zeros(UInt32, 1000000)

# initialize by an array with array-length
# init_key is the array for initializing keys
# key_length is its length
numbers[1] = 19650218 & 0xffffffff

# initializes mt[N] with a seed
for i in 2:N
    numbers[i] = (1566083941 * (xor(numbers[i-1], numbers[i-1] >> 30)) + i) & 0xffffffff
end

println("Number of generating psude random numbers: ", length(numbers)-N)

# generates a random number on [0, 0xffffffff] - interval
for i in 1:(length(numbers)-N)
    num = (numbers[i+1] & 0x7fffffff) + (numbers[i] & 0x80000000)
    if (num & 0x1) == 0
                # ⊻: 排他的論理和(xor)
        numbers[i+N] = numbers[i+M] ⊻ (num >> 1)
    else
        numbers[i+N] = numbers[i+M] ⊻ ((num >> 1) ⊻ a)
    end
end

const NUM_BINS = 100
histogram(numbers.%NUM_BINS, bins=NUM_BINS, xlims=(0,NUM_BINS))
savefig("mt19937.png")

実行例

　　　　　　　　　　図：メルセンヌツイスタで生成した乱数の分布

生成した1000000個の乱数を500個のビンを持つヒストグラムに入れて分布を見ます。一様分布していることがわかります。

疑似乱数をn次元にプロットすることで、品質を確認することができます。たとえば、線形合同法とメルセンヌ・ツイスタで生成した10万個の乱数を3次元にプロットすると以下のようになります。メルセンヌ・ツイスタは3次元空間全体を一様に埋め尽くしていますが、線形合同法はそうではありません。これは線形合同法は周期が短いため、ある決まった大きさの格子の頂点にのみ値が出てしまうからです。

線形合同法とメルセンヌツイスタで発生させた乱数を3次元にプロットするjuliaコード

using Random
using Plots

# 発生させる個数の設定（3次元でプロットするので3で割れる数字）
num_generate_points = 100000;
num_generate_points = num_generate_points - (num_generate_points % 3)
points_3d=trunc(Int, num_generate_points/3);

# 乱数発生
seed = 1234;
# 
println(num_generate_points, " random numbers are generated")
@time rng = MersenneTwister(seed);
gen_rands = rand!(rng, zeros(num_generate_points));

# プロット
conv_to_3d=reshape(gen_rands, points_3d, 3);
scatter(conv_to_3d[:,1], conv_to_3d[:,2], conv_to_3d[:,3], markersize=1, label="mersenne_twister");
savefig("plot_random_numbers.png");

# 線形合同法
senkei_rand = zeros(num_generate_points)
senkei_rand[1]=seed
for i in 2:num_generate_points-1
    # global r = mod(1664525 * r + 1013904223, 2^32)
    # senkei_rand[i+1] = mod(1664525 * senkei_rand[i] + 1013904223, 2^32)
    senkei_rand[i+1] = mod(1103515245 * senkei_rand[i] + 12345, 2^32)
end
print(senkei_rand)

# プロット
conv_to_3d=reshape(senkei_rand, points_3d, 3);
scatter(conv_to_3d[:,1], conv_to_3d[:,2], conv_to_3d[:,3], markersize=1, label="linear_congruential");
savefig("plot_random_numbers_senkei.png");

実行例

　　
　　　　　　図：線形合同法　　　　　　　　　図：メルセンヌ・ツイスタ

Julia のrand()関数

Julia のrand()関数の中身は何なのかを調べてみます。

Random Numbers · The Julia Language

結論としてはXoshiro256++というものでなので安全ですが、「言語のバージョンによって異なるかもしれない¹¹」とのことです。また、メルセンヌ・ツイスタを使うこともできます。乱数生成を行う場合は、Juliaだけでなく、その他の言語でも注意して乱数生成の関数を使うことを心がけてください。

演習

Random Numbers · The Julia Languageで示された4種類の疑似乱数発生器のMersennneTwiter以外のものを用いて10万個の乱数を発生させ、結果を3次元上にプロットせよ。

モンテカルロ・シミュレーション

モンテカルロ・シミュレーションは、前述のように、乱数を用いてある現象の統計的特性を得るためサンプリングを多数回行うシミュレーション手法です。たとえば、コイン投げを繰り返した場合の挙動を調べるのに、区間[0,1]で一様分布する擬似乱数で生成した多数の乱数を入力に使う、などです。

このシミュレーションの概念やアルゴリズムは、利用するモデル化の部分を別にすると比較的単純です。しかし、一般には、良い近似値を得るために多くの乱数を必要とするため、1つの乱数の処理時間が長いと、全体のシミュレーション時間が非常に大きくなります。つまり、乱数の生成がシミュレーション時間全体の短縮の阻害要因となりえます。

ランダム・ウォーク

ランダムウォークは、ある空間上のランダムなステップの連続からなる経路を記述するランダムプロセスです。物理学における分子のブラウン運動や金融工学におけるブラック・ショールズ・モデルなどを始めとする、広い分野で応用されています。

以下に教科書のPythonプログラムをJulia言語に移植したものを示します。

ランダムウォークをモンテカルロシミュレーションするjuliaコード

using Random
using Plots

# timestep
n = 100

x = 0.0
y = 0.0
xlist = [x] # x座標リスト
ylist = [y] # y座標リスト

t0 = time();
for i in 1:n
    global x += (rand() - 0.5) * 2
    global y += (rand() - 0.5) * 2
    push!(xlist, x)
    push!(ylist, y)
end
println(time() - t0, " sec")

# 計算結果の描画
margin=1
plot(aspect_ratio=1.0,
    xlim=(findmin(xlist)[1] - margin, findmax(xlist)[1] + margin),
    ylim=(findmin(ylist)[1] - margin, findmax(ylist)[1] + margin)
    )
anim = Animation()
anim = @animate for i in 1:n
    plot!(xlist[1:i], ylist[1:i], markercolor=:blue, linecolor=:blue, label="", )
end

file_name = "random_walk_.gif"
@time gif(anim, file_name, fps = 4)

実行例

　　　　　図：モンテカルロ・シミュレーションを用いたランダム・ウォークの模擬（再掲）

円周率

モンテカルロ・シミュレーションの代表的かつ実用的(?)なものに、円周率を求めるシミュレーションがあります。これは、一辺が長さ1の正方形の内側に内接する1/4の円を描き、そこにランダムに点をN個発生させる。発生させた点のうち、円の中に入る点の数Sを数える、というものです。ランダムな点を多数発生させれば、N は正方形の面積に対応し、S は半径1の単位円の1/4の面積 $\pi/4$ として近似できます。よって、以下の式から $\pi$ の近似値が求まります。

$\frac{S}{N} \simeq \frac{\pi / 4}{1} = \frac{\pi}{4}$

この方法を使って精度良く円周率を計算するためには、 $1.1 \times 10^5$ 回程度の点を打つする必要があります。詳しくは、モンテカルロ法と円周率の近似計算 - 高校数学の美しい物語などを見てみてください。

以下に、モンテカルロ・シミュレーションを用いて円周率を近似するJuliaコードを示します。

円周率を近似するモンテカルロシミュレーションのjuliaコード

using Random
using Plots

# 試行回数
const TRIALS = parse(Int32, Base.prompt("Please set the number of trials"))

xlist = rand(Float32, TRIALS)
ylist = rand(Float32, TRIALS)

# √x^2 + y^2それが1より大きいか小さいかで判断
points = hypot.(xlist, ylist)
count = 0
for i in points
    if i <= 1
        global count += 1
    end
end

# 円周率の算出
my_pie = (count / TRIALS) * 4.0
println(my_pie)

# 結果の描画
cx = range(0, 1, length=100)
cy = sqrt.(1 .- cx .^ 2)
plot(aspect_ratio=1.0, xlim=(0.0, 1.0), ylim=(0.0, 1.0))

plot!(cx, cy, label="", linewidth=2)
anim = Animation()
anim = @animate for i in 1:TRIALS
    plot!(xlist[1:i], ylist[1:i], markercolor=:blue, seriestype=:scatter, markersize=2, label="")
end

file_name = "compute_pi_with_Monte_Carlo.gif"
@time gif(anim, file_name, fps = 10)

実行例

julia > include("compute_pi_with_Monte_Carlo.jl")
Please set the number of trials: 100
3.4
"/root/compute_pi_with_Monte_Carlo.gif"

　　　　　図：モンテカルロ・シミュレーションを用いた円周率の近似

演習

モンテカルロ・シミュレーションを用いて円周率を近似する。試行回数を[1-10],[10-100],[100-1000],[1000-10000],[10000-100000]のそれぞれの閉区間で10等分し、それぞれの試行回数と円周率の近似値の推移を考察せよ。

以上です。